给两种勾股定理的证明方法勾股定理的证明方法3种

给两种勾股定理的证明方法

勾股定理的证明方法有多种。以下是两种常见的证明方法：

1. 几何证明：通过使用几何图形，如直角三角形和平行四边形，来证明勾股定理。这种证明方法通常利用几何性质和图形的面积关系来推导出勾股定理。

2. 代数证明：通过使用代数运算和方程来证明勾股定理。这种方法通常通过将直角三角形的边长代入三角函数的定义，并使用三角函数的性质和三角恒等式进行推导。

这只是一些常见的证明方法，还有其他更复杂的方法和变种。不同的证明方法可能适用于不同的情况和问题，选择适合的方法取决于问题本身以及证明的目标和要求。

勾股定理的证明方法3种

1、嘿，大家好！今天咱们聊聊勾股定理的证明方法，勾股定理超简单：在一个直角三角形里，两条直角边的平方和等于斜边的平方，数学上就是 \( a^2 + b^2 = c^2 \)，下面分享三种超酷的证明，每种都超直观，保证你一听就懂！

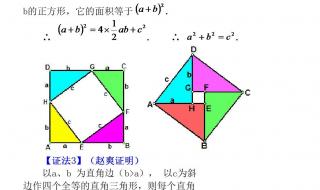
2、第一种：毕达哥拉斯的几何拼图法，想象一下，我们画个大正方形，边长是 \( a + b \)，然后在里面塞进四个完全一样的直角三角形（直角边是 \( a \) 和 \( b \)），它们拼在一起后，中间空出个小正方形，边长正好是斜边 \( c \)，现在算面积：大正方形面积是 \( (a+b)^2 \)，它也等于四个三角形面积加中间小正方形面积，四个三角形面积是 \( 4 \times \frac{1}{2} a b = 2ab \)，小正方形面积是 \( c^2 \)，\( (a+b)^2 = 2ab + c^2 \)，展开左边： \( a^2 + 2ab + b^2 = 2ab + c^2 \)，两边减掉 \( 2ab \)，就得出 \( a^2 + b^2 = c^2 \)，搞定！这方法像玩积木，超有趣。

3、第二种：欧几里得的相似三角形法，这次，从直角顶点画条高到斜边，把斜边 \( c \) 分成两段 \( p \) 和 \( q \)，这样，原三角形被拆成两个小直角三角形，神奇的是，这两个小三角形都和原三角形相似！一个小三角形和原三角形的对应边比例相等： \( \frac{a}{c} = \frac{p}{a} \)，所以 \( a^2 = c \times p \)，同样，另一个小三角形： \( b^2 = c \times q \)，把这两个等式加起来： \( a^2 + b^2 = c p + c q \)，右边是 \( c (p + q) \)，而 \( p + q \) 就是斜边 \( c \)，所以 \( a^2 + b^2 = c^2 \)，这方法靠比例关系，超巧妙。

4、第三种：坐标几何法（超快代数版），把三角形放在坐标系里：直角在原点 \( (0,0) \)，一个点放在 \( (a,0) \)，另一个在 \( (0,b) \)，斜边是从 \( (a,0) \) 到 \( (0,b) \)，用距离公式算斜边长： \( c = \sqrt{(a-0)^2 + (0-b)^2} = \sqrt{a^2 + b^2} \)，两边平方，直接得出 \( c^2 = a^2 + b^2 \)，这方法简单粗暴，适合懒人，两秒搞定！三种证明各有特色，试试看，数学原来这么好玩！